Sistema Hexadecimal

El sistema hexadecimal es el sistema de numeración posicional que tiene como base el 16.

Sus números están representados por los 10 primeros dígitos de la numeración decimal, y el intervalo que va del número 10 al 15 están representados por las letras del alfabeto de la ‘A’ a la ‘F’.

Su uso actual está muy vinculado a la informática y ciencias de la computación donde las operaciones de la CPU suelen usar el byte u octeto como unidad básica de memoria.

Aunque los circuitos electrónicos digitales y las computadoras utilizan el sistema binario, el trabajar con este sistema de numeración es bastante más complicado, lo que da como resultado una gran posibilidad de cometer errores se trabaja con números binarios demasiado largos.

Este sistema posee dos grandes ventajas en el entorno informático:

1. Crea una simplificación en la escritura de los números decimales, ya que cada 4 cifras binarias se representa simplemente por una hexadecimal.
2. Cada cifra hexadecimal se puede expresar por 4 cifras binarias, con lo que la transposición entre estos dos sistemas se facilita considerablemente. Para convertir un numero binario a hexadecimal se realizará el mismo proceso pero de forma inversa.

A continuación dejaremos una tabla en la que se observan cómo se representa cada número decimal en binario y hexadecimal. Si no sabes o quieres repasar, en el anterior artículo hablamos sobre el sistema binario, comentando qué es, como se utiliza y el pasaje de números binarios a decimales.

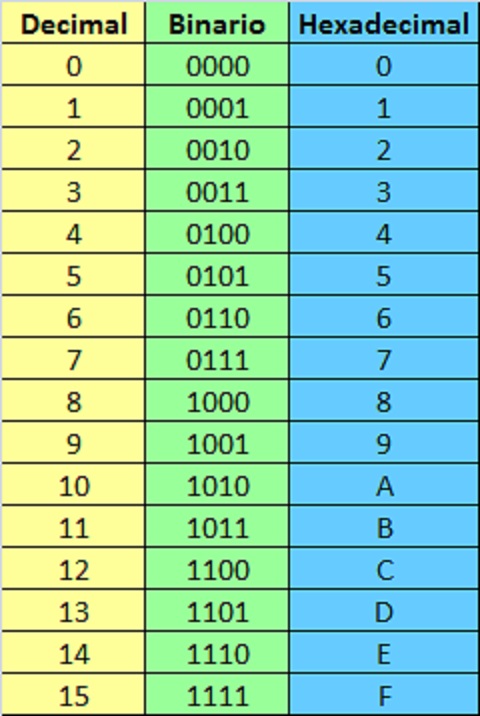
Alguno ejemplos de conversión

Ejemplo 1

Queremos convertir el número hexadecimal A6D₁₆ a binario. Cómo vimos en la tabla de arriba podemos sacar los datos necesarios:

• A = 1010
• 6 = 0110
• D = 1101

Por lo tanto A6D₁₆ = 1010 0110 1101

Para pasar un número hexadecimal a un número decimal, debemos de multiplicar los números hexadecimales por las distintas potencias de la base 16 que representa cada digito del sistema hexadecimal.

Ejemplo 2

Queremos convertir el número hexadecimal A6D₁₆ a decimal:

A6D = 10x16² + 6x16¹ + 13x16⁰ = 2560 + 96 + 13 = 2669

Por lo tanto A6D₁₆ = 2669

De forma contraria se obtendrán la conversión de número decimal a hexadecimal. Debemos de dividir por 16 sucesivamente hasta no poder realizarlo más. El número resultante estará constituido por el último cociente seguido de todos los restos.

[anuncio_b30 id=3][anuncio_b30 id=4]

Ejemplo 3

Queremos convertir el número decimal 350 a hexadecimal:

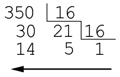
Cómo vemos en la imagen:

• 350 dividido entre 16 da como cociente 21 y resto 14
• 21 dividido entre 16 da como cociente 1 y resto 5

Cómo dijimos antes, primero se toma el cociente final (1) y luego los restos de forma sucesiva de atrás para adelante (5 y 14). Recordando que 14 = E.

Por lo tanto 350 decimal = 15E hexadecimal.

Si quieres conocer otros artículos parecidos a Sistema Hexadecimal puedes visitar la categoría Electrónica digital.