¿Qué dice el Teorema de Pitágoras?

En la antigua Grecia entre los años 569 y 475 antes de cristo vivió un filósofo y matemático llamado Pitágoras de Samos, es considerado por la historia como el primer matemático puro, pues contribuyó de una manera bastante significativa al avance de la denominada matemática helénica, la geometría y hasta la aritmética.

Uno de los grandes descubrimientos de este matemático fue el denominado como Teorema de Pitágoras, un cálculo que establece ciertos parámetros para conocer cómo están relacionados todos los lados de un triángulo rectángulo.

Este teorema nos proporciona uno de los vínculos más importantes entre la geometría y el álgebra pues nos permite calcular fácilmente las distancias entre los lados de estos triángulos en términos de coordenadas.

Los estudios de Pitágoras inspiraron a las disposiciones básicas de la ciencia que más adelante sería definida como “Trigonometría” y establecieron las bases que posibilitaron la exploración del planeta tierra, instituyendo la topografía, y facilitando la navegación.

Ahora bien, en los tiempos más recientes el Teorema de Pitágoras ha permitido el estudio de la relatividad general y la relatividad espacial, ambas clasificadas como las teorías más importantes para explicar el tiempo y la gravedad en nuestro mundo.

¿Cuál es la fórmula del Teorema de Pitágoras?

Para establecer que en todo triangulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, Pitágoras de Samos se valió de la fórmula siguiente:

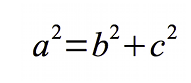
A partir de esta ecuación se deducen tres corolarios que permiten la verificación algebraica de la fórmula y su aplicación práctica, los cuales son:

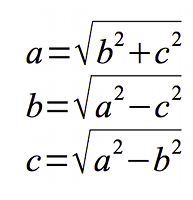
Resolviendo estos cálculos es muy simple demostrar la eficacia del Teorema de Pitágoras.

Demostraciones del Teorema de Pitágoras

Una de las demostraciones más usadas para enseñar la validez de esta fórmula es la de El Zhoubi Suanjing y el Jiuzhang Suanshu Pappus esta data aproximadamente del 500 y el 300 antes de cristo, esta obra se cree que no fue conocida por Pitágoras, pero demuestra fielmente su teorema de la forma siguiente:

Partiendo de un triángulo rectángulo se construye un cuadrado de lado (a + b) que se parte en un total de cuatro triángulos de base a, y altura b, además de un cuadrado de lado c.

A continuación, puedes ver gráficamente la demostración hecha en el Zhoubi Suanjing. En la que a = 3, b = 4 y c = 5.

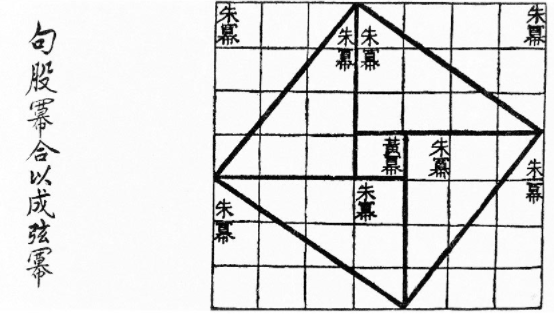
Explicando de una forma más exhaustiva esta demostración del Teorema de Pitágoras se puede decir que:

Sea el triángulo rectángulo de catetos a y b con hipotenusa c. Hay que comprobar el área del cuadrado del lado c sea igual a la suma de las áreas de los cuadrados del lado a y b, siguiendo la fórmula de Pitágoras de:

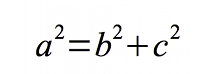
A partir de este punto se añaden tres triángulos iguales al original dentro del cuadrado del lado c, formando de esta manera una figura como la mostrada en la imagen anterior. Con esto se obtiene un cuadrado de menor tamaño, en el que se puede observar que efectivamente tiene un lado de b – a.

Luego de esto el área puede expresarse así:

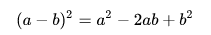
Esto debido a que:

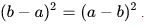
Sabiendo esto, resulta evidente que el área del cuadrado del lado c es la suma del área de los cuatro triángulos rectángulo, que tienen altura a y base b. Los que se encuentran dentro de él más el área del cuadrado menor.

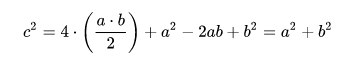
Y con esta fórmula queda efectivamente demostrado el Teorema de Pitágoras.

Conclusión

Gracias al Teorema de Pitágoras y los hechos que prueba es que en la actualidad muchas ramas científicas se encuentran tan avanzadas en el estudio de la forma y disposición de nuestro planeta, brindando explicaciones a la mayoría de fenómenos presentes en él.