Operaciones Con Números Complejos

Antes de entrar de lleno en las operaciones con números complejos, vamos a comenzar por el principio.

Los números complejos, a diferencia de lo que muchos piensan, son muy utilizados para resolver problemas reales en el campo de la ingeniería e incluso en la física. Está la creencia que solo son una invención para resolver las raíces de número negativos, y que no tienen aplicación práctica en la vida real.

Lamento decirte que esa es una creencia muy muy errada. 🤷‍♂️

Pero entonces, ¡Vamos por pasos!

▷ ¿Qué son los Números Complejos?

Los Números Complejos son un par ordenado de números reales, donde a una de sus partes se la denomina «parte real» y a otra «parte imaginaria» y forman parte de un conjunto numérico que contiene la totalidad de los números reales.

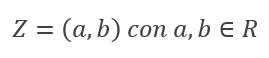
En cuanto a la forma de expresarlos, se los suele representar como la suma de la parte real y la parte imaginaria, a este tipo de representación se la denomina forma polar de un numero complejo.

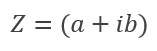
▷ Conjugado de un Número Complejo

Todo numero complejo tiene su conjugado, pero ¿que es exactamente esto?, bueno el conjugado de un numero complejo es el mismo numero pero con la parte imaginaria opuesta, es decir que se le cambia el signo en la forma polar.

Siempre, el conjugado de un número complejo será simétrico respecto del eje real. gráficamente sería lo siguiente.

▷ Unidad imaginaria de un Número Complejo

Acá esta la magia de todo, la unidad imaginaria es representada por la letra i. y tiene la particularidad que al elevarlo al cuadrado da como resultado menos uno.

Esto es una de las bases fundamentales de los números complejos, permite resolver raíces de polinomios que no tienen respuesta en el conjunto de los reales.

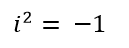
▷ Operaciones con números complejos

Las operaciones con números complejos que se pueden realizar son las mismas que en los números reales, es decir se pueden realizar sumas, restas, multiplicaciones y divisiones.

➛ Suma de complejos

Sumar números complejos es muy simple, es igual que lo hacemos con los vectores, donde sumamos miembro a miembro, es decir sumamos la parte real de uno con la del otro y la parte imaginaria de uno con el del otro, pero vamos con un ejemplo para que se entienda mejor.

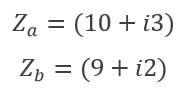
Para sumar estos dos complejos, como dije anteriormente, tenemos que hacerlo miembro a miembro, por un lado la parte real y por otro la parte imaginaria, el resultado que nos queda es el siguiente.

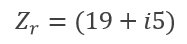
➛ Resta de complejos

Bueno, es igual de simple que la suma, tendremos que restar miembro a miembro y listo, supongamos que queremos restar los dos números complejos anteriores, nos quedaría lo siguiente.

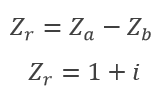
➛ Multiplicación de complejos

Dado que estamos multiplicando dos binomios, tenemos que hacer uso de la propiedad distributiva. El producto de dos números complejos es un numero complejo.

Vamos con un ejemplo.

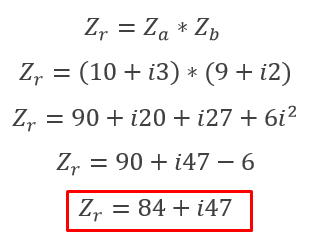
➛ División de dos números complejos

Esta operatoria es un poco mas difícil que la suma y la resta que vimos anteriormente, así que vamos por pasos.

Supongamos que queremos realizar la siguiente operación de división, el secreto está en multiplicar y dividir por el conjugado del complejo del denominador.

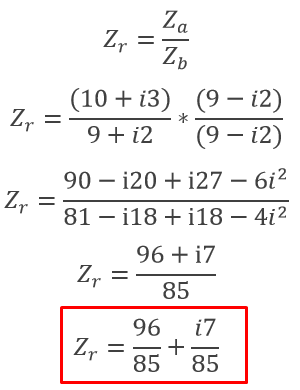
Dividir dos números complejos no es algo difícil de hacer, pero muchas veces puede resultar laborioso, lo importante es que aprendamos el procedimiento.

▷ Representación gráfica de un número complejo

Para representar gráficamente a un número complejo, en el eje horizontal vamos a representar la coordenada Real mientras que en el eje vertical vamos a representar la parte imaginaria, el punto de intersección entre ambas coordenadas va a ser el número complejo representado.

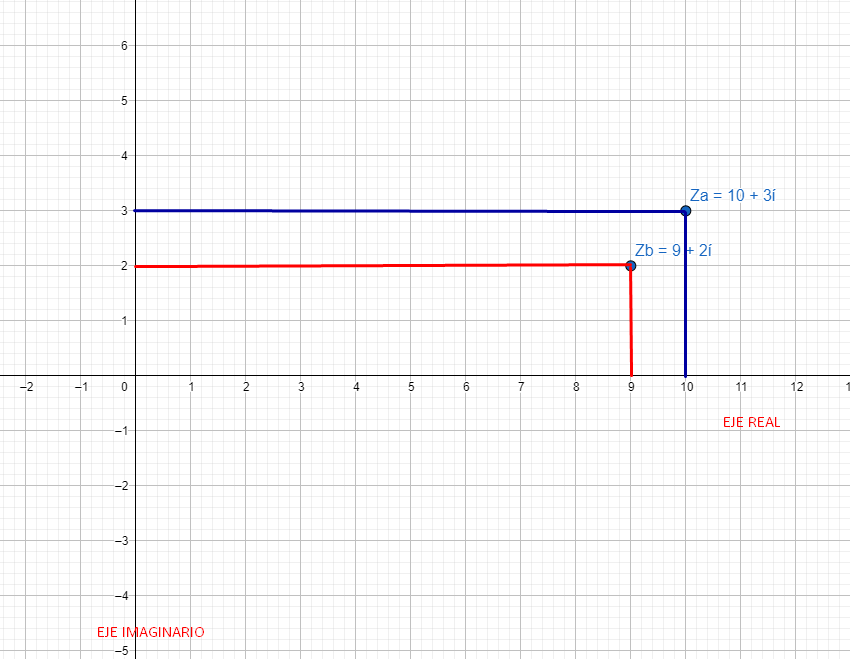
Miremos con atención la imagen anterior, estoy graficando los dos números que trabajamos a modo de ejemplo a lo largo de todo el artículo.