MÉTODO DE DETERMINANTES O MÉTODO DE CRAMER

El Método de determinantes es una forma de resolución de sistemas de ecuaciones lineales, al igual que los métodos sustitución e igualación, este método permite obtener el resultado de un sistema de ecuaciones en unos simples pasos.

La ventaja mas resonante de utilizar este método es que su automatización, entendiendo esto como una forma de resolver ecuaciones de forma metodológica, nos olvidamos de despejes y demás.

La forma mas practica de entender el procedimiento es mediante un ejemplo.

EJEMPLO DE RESOLUCIÓN

Supongamos que tenemos que resolver la siguiente ecuación, donde nos piden encontrar los valores de X e Y que cumplen con esas condiciones.

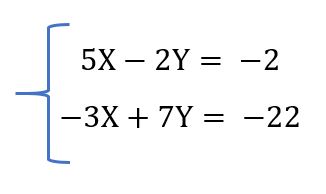
Para resolverlo utilizando el método de determinantes, tenemos que siempre resolver los siguientes cálculos, para todos los sistemas de ecuaciones independientemente de sus valores, las resolución es siempre la misma y hay que plantear lo siguiente.

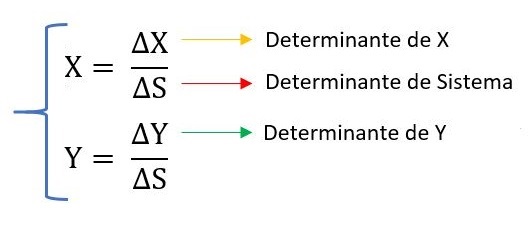
Pero, ¿Cómo calculo los determinantes de X,Y y el del sistema? muy simple, de la siguiente manera.

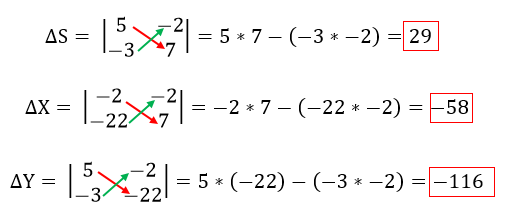
1. Para Calcular el determinante del sistema ΔS, Armamos el determinante solo con los valores que están multiplicando a la X y la Y. Es por eso que nos queda la estructura que vimos arriba, luego multiplicamos cruzados, y restamos los múltiplos.
2. Para Calcular el determinante de X ΔX  lo que tenemos que hacer es armarnos el determinante con los valores que están a la derecha del signo igual, y con los valores que están multiplicando a la Y. De esta forma obtenemos el determinante que vimos arriba. luego la operatoria es la misma, multiplicamos cruzado y restamos las multiplicaciones.
3. Para Calcular el determinante de Y ΔY  lo que tenemos que hacer es armarnos el determinante con los valores que están a la derecha del signo igual, y con los valores que están multiplicando a la X. De esta forma obtenemos el determinante que vimos arriba. Luego la operatoria es la misma, multiplicamos cruzado y restamos las multiplicaciones.

Ahora que ya tenemos los valores de los determinantes, lo que sigue es encontrar los valores correspondientes a X e Y, y de esa forma resolvemos la ecuación. Para eso debemos hacer uso de las formulas que están en la segunda imagen.

Es decir que para calcular el valor de X tenemos que dividir el determinante de X con el Determinante del sistema y para encontrar el valor de Y tenemos que dividir el determinante de Y con el determinante del sistema.

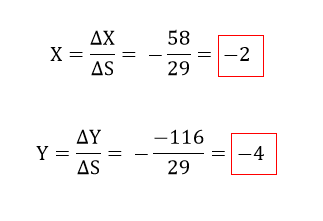
Obviamente, en matemática existen muchas formas de hacer lo mismo, existen varios métodos de resolución de ecuaciones, el método de determinantes no es el único, existe el método de igualación o el método de sustitución, en fin podemos utilizar el método que mas fácil nos resulte 🙂