MÁQUINAS SIMPLES – POLEAS
En el artículo anterior, pudimos observar a las máquinas simples como palanca y torno. En este, nos concentraremos sobre la función de las Poleas.
¿QUÉ ES UNA POLEA?
Una polea es un disco que puede girar alrededor de su eje. En su borde posee una canaladura en la que se aloja un cable, una cuerda o una cadena.
La polea se emplea para elevar cargas.
SI el eje es fijo, es decir si la polea solamente gira, se llama polea fija.
Si la polea se desplaza juntamente con la carga que eleva, se llama polea móvil.
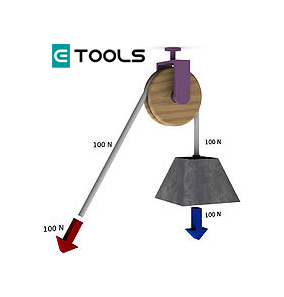
POLEA FIJA - CONDICIÓN DE EQUILIBRIO
Observemos que cuando la polea fija está en equilibrio podemos reemplazarla por la palanca indicada en la figura, cuyo apoyo coincide con el eje y los brazos de la palanca con los radios de la polea.
La condición de equilibrio será:
La polea fija está en equilibrio cuando la potencia es igual a la resistencia.
Esta condición se cumple cualesquiera sean las direcciones de las ramas de la cuerda.
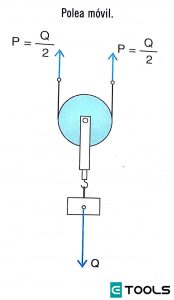
POLEA MOVIL - CONDICIÓN DE EQUILIBRIO
Observemos que cuando esta polea está en equilibrio podemos reemplazarla por la palanca de la figura, en la que el brazo de potencia es a = 2r y el de resistencia es b = r.
La ecuación de equilibrio es:
La polea móvil está en equilibrio cuando la potencia es igual a la mitad de la resistencia.
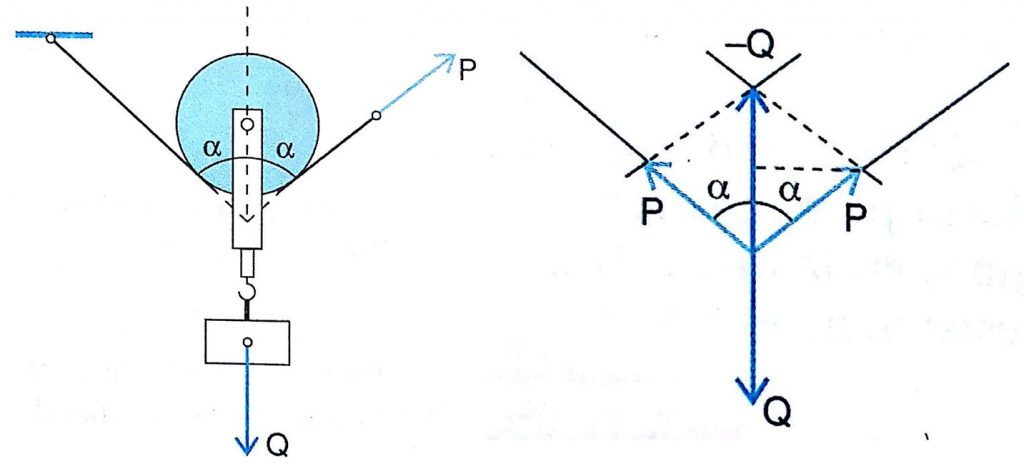
Por lo anterior, se deduce que Q es la equilibrante de los esfuerzos realizados por ambas cuerdas, los que son iguales.
Esta condición se cumple solamente si las dos ramas de la cuerda son paralelas. Si no lo fueran, para hallar la potencia deberíamos descomponer la fuerza opuesta a la resistencia aplicando la regla del paralelogramo, ya que Q es la equilibrante del sistema formado por las dos fuerzas P de igual intensidad.
Teniendo en cuenta el triángulo rectángulo indicado en la figura, ya que el paralelogramo es un rombo, resulta:
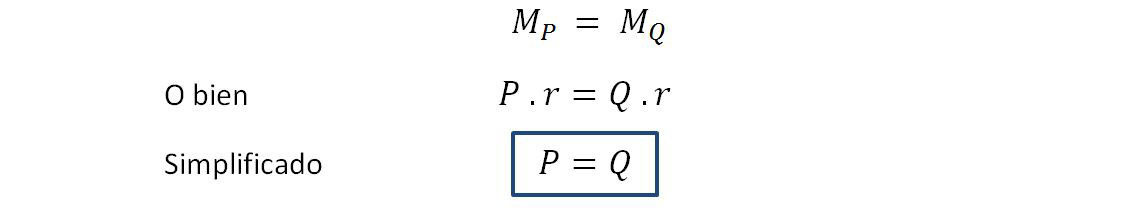
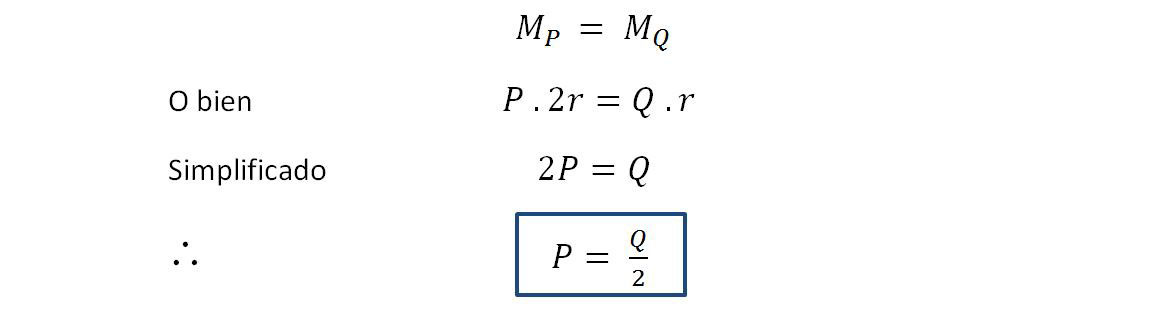
Deja un comentario