
MÁQUINAS SIMPLES - PALANCA y TORNO

¿A QUE DENOMINAMOS MÁQUINAS SIMPLES?
El hombre con el afán de minimizar sus esfuerzos, a lo largo del tiempo y de la historia fue capaz de utilizar el razonamiento para desarrollar sistemas de ayuda que se conocen como maquinas simples.
En este articulo comenzaremos a explicar algunos de estos dispositivos, los mas comunes y mas conocidos por todos son la palanca, el torno, el plano inclinado, las poleas y sus combinaciones, que reciben el nombre de Máquinas Simples.
PALANCA
Un cuerpo rígido que puede oscilar alrededor de un eje fijo, constituye una palanca.
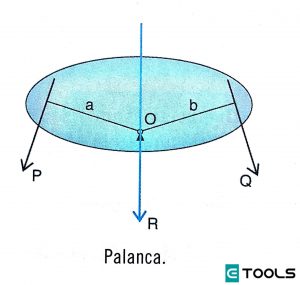
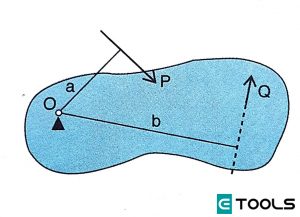
Consideramos un cuerpo rígido que puede oscilar alrededor de Ο (apoyo), sobre el que actúan las fuerzas P (potencia) y Q (resistencia). Estará en equilibrio cuando la resultante R de P y Q pase por Ο, pues su así no fuera, la fuerza R haría girar la palanca alrededor de Ο.
Por lo visto cuando la palanca está en equilibrio, la suma algebraica de los momentos de Q y P con respecto de Ο será nula, ya que Ο es un punto de la recta de acción R.
Para que esta condición se cumpla los dos momentos deben ser iguales en valor absoluto, por lo que podemos escribir (haciendo abstracción del signo):
Lo que nos permite expresar la condición de equilibrio de la palanca.
La palanca esta en equilibrio cuando el momento de la potencia es igual al momento de la resistencia, en valor absoluto.
"a se llama brazo de potencia, b brazo de resistencia y ambos, brazos de palanca."
Es importante notar que los momentos son iguales en valores absolutos, pero de distinto signo para que la palanca esté en equilibrio.
En el ejemplo que comentamos la palanca estará en equilibrio si se cumple la siguiente relación.
TORNO
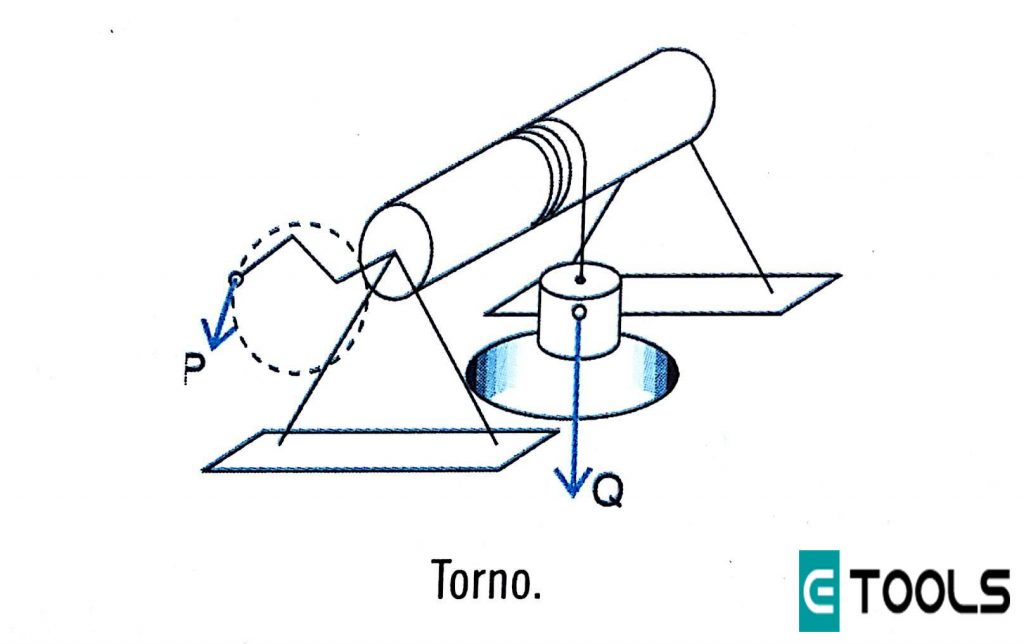
Un cuerpo cilíndrico de eje horizontal, accionado por una manivela, constituye un torno.
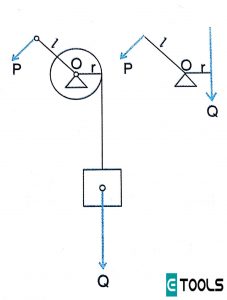
Cuando el torno esta en equilibrio, se lo puede reemplazar por la palanca de la figura que se muestra mas abajo, cuya condición de equilibrio es la siguiente
Donde l es la longitud de la manivela y r el radio del cilindro.
REFERENCIAS
- Libro física universitaria sears zemansky young freedman volumen 1
Si quieres conocer otros artículos parecidos a MÁQUINAS SIMPLES - PALANCA y TORNO puedes visitar la categoría Fisica.
Deja un comentario
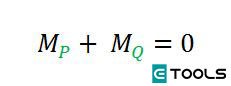
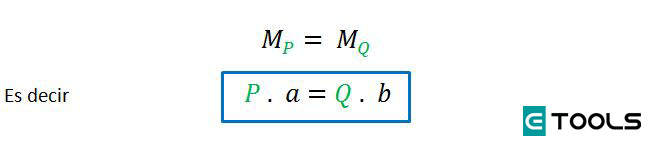
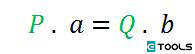
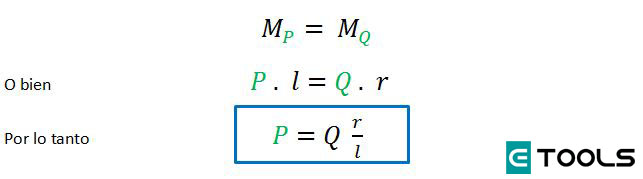





EXCELENTE, DEBEN COLOCAR OTROS TEMAS DE FÍSICA GRACIAS. Enviarme novedades por favor. gracias.