
FACTORIZACIÓN DE POLINOMIOS DE GRADO 2
QUE ES FACTORIZAR UN POLINOMIO DE GRADO 2
Factorizar no es ni mas ni menos que expresar un numero como la multiplicación de otros números menores por los cuales se pueda dividir. Puede sonar complicado, pero la realidad es que es muy simple, el siguiente ejemplo demuestra la simpleza del concepto.
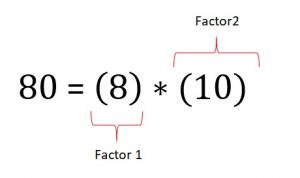
Supongamos que queremos factorizar el numero 80, ¿como lo expresaríamos?, como la multiplicación de 8 por 10. Muy simple.
FACTORIZAR UN POLINOMIO DE GRADO 2
Ya vimos que significa Factorizar, entonces ¿a que se refieren los profesores cuando nos piden factorizar un polinomio de grado 2?, lo que nos están pidiendo es que expresemos ese mismo polinomio con multiplicación de polinomios de grado 1, es el mismo concepto. Miremos el siguiente ejemplo.
COMO FACTORIZAR UN POLINOMIO DE GRADO 2
Para hacerlo de forma practica y segura tenemos que hacer uso de una formula, en la mayoría de los institutos educativos se la enseña como la formula "resolvente", aunque su nombre original es formula de "Bhaskara", que fue deducida por el matemático indio Bhaskaracharya.
La formula que tenemos que utilizar es la siguiente, esta formula nos dará dos resultados, cada uno de ellos representan las raíces de la función original, es decir donde el polinomio original es igual a cero.
Veamos un ejemplo, utilicemos el mismo polinomio que planteamos anteriormente y supongamos que nos piden factorizarlo.
Lo primero que tenemos que hacer, es reemplazar los coeficientes de nuestro polinomio en la formula resolvente (números que multiplican a la x y el termino independiente).
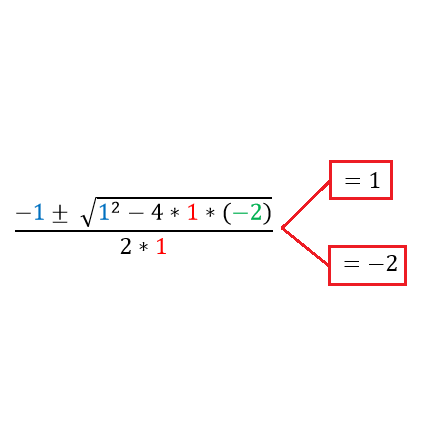
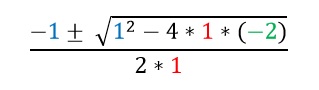
En nuestro ejemplo a = 1; b = 1; c = -2, identificado esto el paso siguiente es colocarlos en la formula resolvente, como en la imagen siguiente.
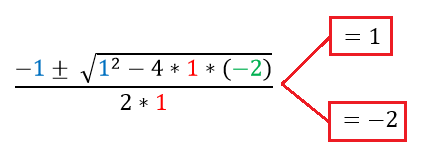
Esta ecuación nos entrega dos resultados, como dijimos antes, son las raíces o ceros de la función.
¿Que significa ese resultado?, que al reemplazar el polinomio por x = 1 o por x = -2 el polinomio da como resultado cero.
Ahora el paso siguiente es armar la multiplicación, de factores, este es el paso mas simple, solo tenemos que colocar (x - resultado obtenido) y multiplicarlo entre si, es decir hacer lo que muestro en la siguiente imagen.
Listo, esa multiplicación de factores es el polinomio factorizado, para verificar que esta bien echo, simplemente tenemos que hacer la multiplicación, y nos debería quedar el mismo polinomio que teníamos al inicio.
Si quieres conocer otros artículos parecidos a FACTORIZACIÓN DE POLINOMIOS DE GRADO 2 puedes visitar la categoría Matemática básica.


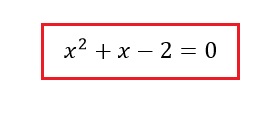
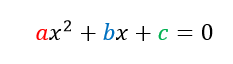
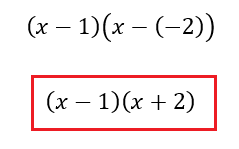
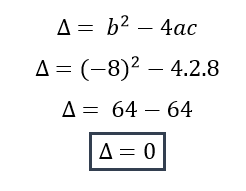


Deja un comentario