
ENERGÍA CINÉTICA: TEOREMA DEL TRABAJO Y ENERGÍA (PARTE 1)
TRABAJO Y ENERGÍA
El trabajo total realizado por fuerzas externas sobre un cuerpo se relaciona con el desplazamiento de éste (los cambios en su posición), pero también está relacionado con los cambios en la rapidez del cuerpo. Para comprobarlo, observaremos la siguiente imagen:
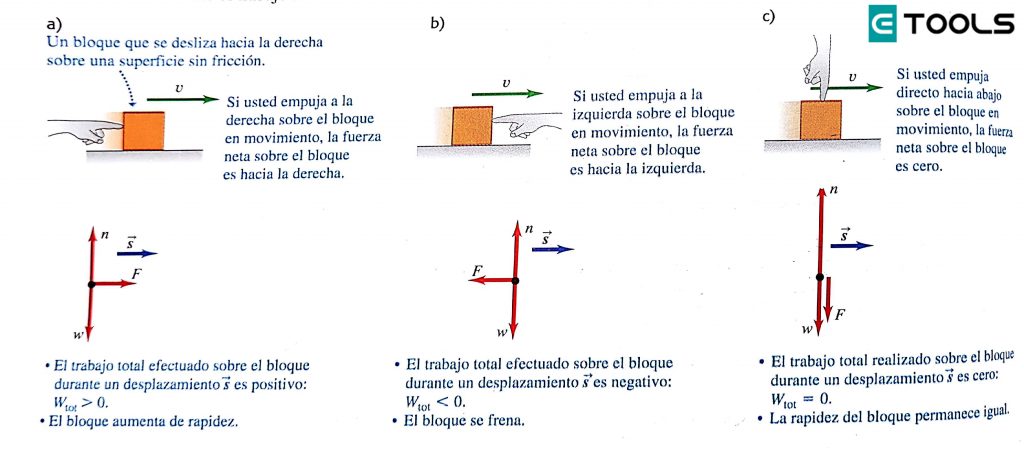
Se muestra tres ejemplos de un bloque que se desliza sobre una mesa sin fricción. Las fuerzas que actúan sobre el bloque son su peso , la fuerza normal y la fuerza ejercida por la mano.
En la imagen, la fuerza neta sobre el bloque es en la dirección de su movimiento. Por la segunda ley de Newton, ello significa que el bloque se acelera; nos indica también que el trabajo total Wtot. El trabajo total es negativo en la figura B porque la fuerza neta se opone al desplazamiento; aquí el bloque se frena. La fuerza neta es cero en la figura C, así que la rapidez del bloque no cambia y el trabajo total efectuado sobre él es cero. Podemos concluir que, si una partícula se desplaza, se acelera si Wtot > 0, se frena si Wtot < 0 y se mantiene su rapidez si Wtot = 0.
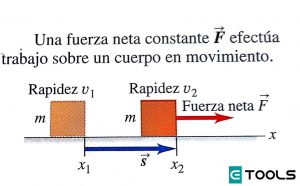
Hagamos más cuantitativas tales observaciones. Considere una partícula con masa que se mueve en el eje +x (como en la figura de arriba). La aceleración de la partícula es constante y está dada por la segunda ley de Newton, . Suponga que la rapidez cambia de a mientras la partícula sufre un desplazamiento del punto al punto . Usando una ecuación de aceleración constante:
El producto es el trabajo efectuado por la fuerza neta y, por lo tanto, es igual al trabajo total Wtot efectuado por todas las fuerzas que actúan sobre la partícula. Llamamos la cantidad la energía cinética de la partícula (definición de energía cinética):
Igual que el trabajo, la energía cinética de una partícula es una cantidad escalar; solo depende dela masa y la rapidez de la partícula, no de su dirección de movimiento. Un automóvil (visto como partícula) tiene la misma energía cinética yendo al norte a 10 m/s que yendo al este a 10 m/s. la energía cinética nunca pude ser negativa, y es cero sólo si la partícula está en reposo.
Ahora podemos interpretar la ecuación (1) en términos de trabajo y energía cinética. El primer término del miembro derecho de la ecuación es , la energía cinética final de la partícula(es decir, después del desplazamiento). El segundo término es la energía cinética inicial. , y la diferencia entre estos términos es el cambio de energía cinética. Así la ecuación 1 dice:
El trabajo efectuado por la fuerza neta sobre una partícula es igual al cambio de energía cinética de la partícula:
Este es el resultado del teorema Trabajo-Energía, que continúa en la parte 2.
Si quieres conocer otros artículos parecidos a ENERGÍA CINÉTICA: TEOREMA DEL TRABAJO Y ENERGÍA (PARTE 1) puedes visitar la categoría Fisica.
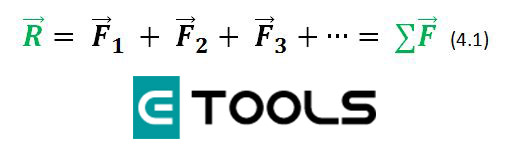

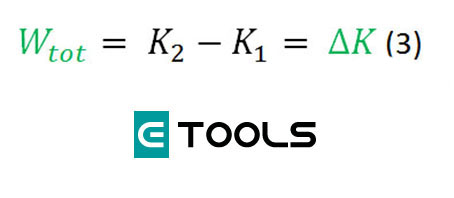





Deja un comentario