
CUANDO DOS RECTAS SON PARALELAS O PERPENDICULARES
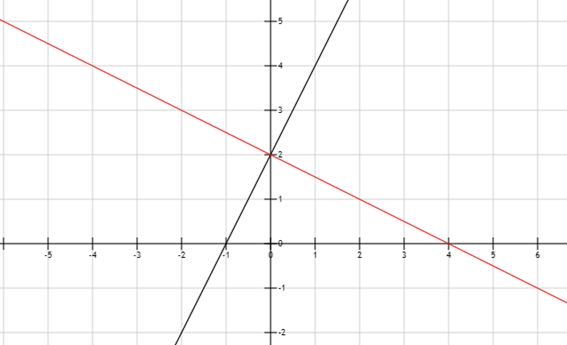
Para trabajar con rectas en el eje cartesiano, primeramente tenemos que conocer la formula genérica de una función lineal, sus variables y cómo se comporta la función al modificarlos.
Sabemos que una función lineal respeta la siguiente formula, donde “m” representa la pendiente y “b” la ordenada al origen.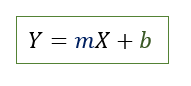
En los casos que m sea negativo, la pendiente será decreciente, a medida que aumente el valor de X, el valor de Y será cada vez más pequeño.
La ordenada al origen, representa el punto donde la recta corta al eje Y, para calcularlo solo tenemos que reemplazar la X con cero, ahí nos queda que b es la ordenada al origen.
VEMOS UN EJEMPLO
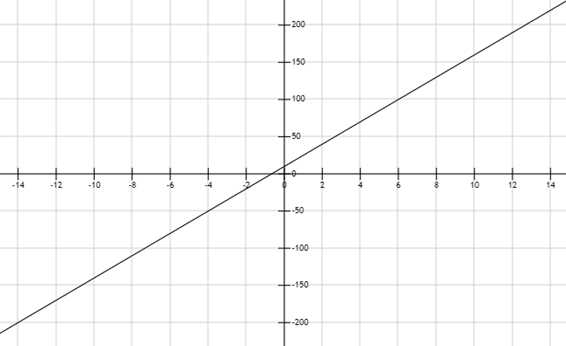
Supongamos que queremos graficár la siguiente función lineal, solo con ver la ecuación ya podemos saber la forma que tendrá.
La ordenada al origen es 10, porque al reemplazar X con cero el valor de Y es 10, ya podemos saber dónde corta la función al eje Y.
También podemos saber que la función es creciente, porque el valor de la pendiente es positivo. Es decir que a medida que aumenta el valor de X también lo hace el valor de Y.
Para graficarla, tenemos dos formas de hacerlo, la primera es darle valores a X para obtener los de Y para luego unir los valores de Y correspondientes.
La otra forma mucho más simple es ver donde la recta corta al eje X y al Eje Y y luego unirlos.
Como dijimos antes, la recta corta al eje Y en 10 (ordenada al origen), para saber dónde la recta corta al eje Y tenemos que reemplazar Y con cero, de manera que nos quede la siguiente ecuación, luego despejamos X y listo.
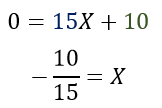
¿CUANDO DOS RECTAS SON PARALELAS?
Es muy simple, para que dos rectas sean paralelas simplemente tienen que tener la misma pendiente, puede tener cualquier ordenada al origen.
Supongamos que queremos encontrar una recta paralela a la anterior que pase por el punto (0,50), es decir que la ordenada al origen tiene que ser 50.
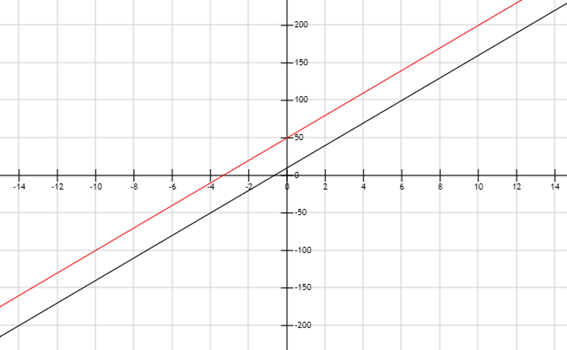
Si graficamos las dos rectas en un mismo eje cartesiano podemos corroborar efectivamente que son paralelas.
¿CUANDO DOS RECTAS SON PERPENDICULARES?
Vale la pena aclarar que una recta es perpendicular a otra cuando el Angulo entre ellas es de 90°. Ahora supongamos que queremos encontrar una recta perpendicular a la primera que pase por el punto (0,50) es decir que la ordenada al origen sea 50, para encontrar una recta perpendicular a otra tenemos que tomar la pendiente de la primera, multiplicarla por (-1) e invertir el número.
Por ejemplo, en la primer recta que calculamos la pendiente era 15, es decir que la perpendicular tendrá la pendiente (-1/15), lo que nos quedara una recta de la siguiente forma.
VEAMOS UN EJEMPLO
Supongamos que tenemos la siguiente recta y queremos encontrar un perpendicular que pase por la misma ordenada al origen.
Al calcular la recta paralela según lo que explicamos antes nos queda la siguiente función.
Al graficarlas podemos ver que efectivamente ambas rectas son paralelas y pasan por la misma ordenada al origen.
CONCLUSIÓN
- Para que una recta sea paralela a otra, la pendiente debe ser la misma.
- Para que una recta sea perpendicular a otra, la pendiente tengo que multiplicarla por -1 e invertirla.
- La ordenada al origen es donde la función corta al eje Y cuando X es igual a cero.
- Si la pendiente es positiva, la función es creciente.
- Si la pendiente es negativa la función es decreciente.
Si quieres conocer otros artículos parecidos a CUANDO DOS RECTAS SON PARALELAS O PERPENDICULARES puedes visitar la categoría Matemática básica.
-
-
Gran información, muchas gracias.
Deja un comentario
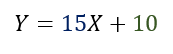
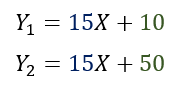
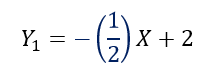
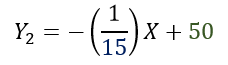


Excelente explicación; súper sencilla y con ejemplos comprobables.. Agradezco la información de este articulo