CONVERSIÓN DE DECIMAL CON DECIMALES A BINARIO

En el artículo anterior hablamos de los números binarios, tanto su definición como el pasaje de un número decimal a binario y viceversa. Ahora, daremos una buena cantidad de ejemplos con distintos problemas para que, al terminar de leer, ya no te quede ninguna duda de cómo poder hacer la conversión sin ningún tipo de inconvenientes.

OPERACIONES POSIBLES QUE SE PUEDEN REALIZAR CON NÚMEROS BINARIOS

El sistema de numeración binario tiene una ventaja muy grande, lo fácil que es realizar cuentas de adición y multiplicación.

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 1 = 10
• 0 x 0 = 0
• 0 x 1 = 0
• 1 x 1 = 1

Ejemplo de adición:

0.111.011.011 + 1.110.010.110 = 101.0111.0001

Ejemplo de multiplicación:

100.111 x 100.101 = 101.1010.0011

CONVERSIÓN DE DECIMAL (CON DECIMALES) A BINARIO

1. El proceso de convertir un número decimal con decimales a binario es casi idéntico al pasaje sin decimales. Para llevar a cabo esta conversión debemos:
2. Se transforma la parte entera a binario (este paso es el que venimos haciendo cuando tenemos números sin decimales)
3. Ahora, se transforma la parte fraccionaria. Al contrario de la parte entera, ahora debemos multiplicar por 2. Si el resultado que obtenemos es mayor o igual a 1 se anotará como un 1 (uno) en binario, de lo contrario, si es menor, se anotará un 0 (cero).

Por último, luego de realizar ambas multiplicaciones, se juntarán los números obtenidos en orden.

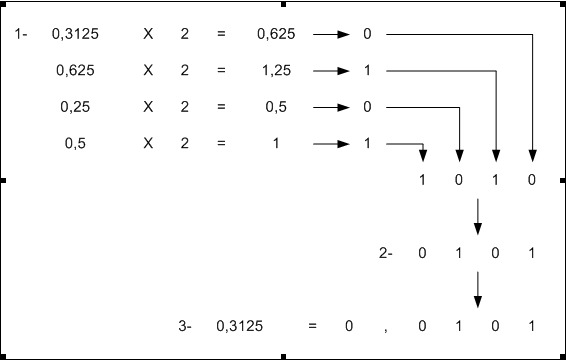
EJEMPLO 1

• 0,8125 (decimal)
• 0,8125 multiplicado entre 2 da como resultado 1,625 (1 en binario)
• 0,625 multiplicado entre 2 da como resultado 1,25 (1 en binario)
• 0,25 multiplicado entre 2 da como resultado 0,5 (0 en binario)
• 0,5 multiplicado entre 2 da como resultado 1,0 (1 en binario)

En orden el resultado es 1101, por lo tanto 0,8125 es 0,1101 en binario

EJEMPLO 2

3,25 (decimal)

Primero, calculamos la parte entera (3) que como bien ya sabemos, es 11 en binario.

Ahora continuamos con la parte decimal

• 0,25 multiplicado entre 2 da como resultado 0,5 (0 en binario)
• 0,5 multiplicado entre 2 da como resultado 1,0 (1 en binario)

Cómo ya nos quedamos sin poder resolver, unimos los números en el orden obtenido:

11 del 3 decimal + 01 del 0,25 decimal = 11,0100 (completamos con 0 hasta llegar siempre a 4 números binarios).

También, podemos encontrarnos con números que son periódicos en el sistema binario, como lo es el 0,1.

0,1 (decimal)

• 0,1multiplicado entre 2 da como resultado 0,2 (0 en binario)
• 0,2 multiplicado entre 2 da como resultado 0,4(0 en binario)
• 0,4 multiplicado entre 2 da como resultado 0,8 (0 en binario)
• 0,8 multiplicado entre 2 da como resultado 1,6 (1 en binario)
• 0,6 multiplicado entre 2 da como resultado 1,2 (1 en binario)
• 0,2 multiplicado entre 2 da como resultado 0,4(0 en binario) <-- Comienza a repetirse
• 0,4 multiplicado entre 2 da como resultado 0,8 (0 en binario)
• 0,8 multiplicado entre 2 da como resultado 1,6 (1 en binario)
• 0,6 multiplicado entre 2 da como resultado 1,2 (1 en binario)

Por lo que el resultado en orden es: 0,0011.0011 y continua repitiéndose infinitamente (binario periódico).