CÓMO CALCULAR EL ÁREA Y EL VOLUMEN DE UN PRISMA RECTANGULAR
En uno de los artículos anteriores, dejamos en claro de que estamos hablando cuando hablamos de prismas, te dejo el link para que lo leas si aun lo lo hiciste, ¿que es un prisma?.
En este articulo vamos a ir un poco mas en detalle, tratare de explicarles como tenemos que hacer para calcular el área y volumen de un prisma rectangular y no morir en el intento. si, exagere un poco, no es para tanto 🙂
Vamos al grano.
CÓMO CALCULAR EL ÁREA DE UN PRISMA RECTANGULAR
El área de un prisma rectangular se calcula conociendo los lados de la base rectangular y su altura, con esos dos datos ya podemos calcular el área y el volumen sin problemas.
Cómo dije en el articulo anterior, Un Prisma Rectangular es un poliedro cuya superficie está formada por dos rectángulos iguales y paralelos entre sí, llamados bases y por cuatro caras laterales que son paralelas e iguales, dos en dos (también son rectángulos).
Para calcular el área tenemos que hacer dos cálculos, primero calcular el Área de la base y luego el Área de las laterales.
CALCULO DEL ÁREA
Cuando hablamos del área de la base nos referimos al "piso" y al "techo" del prisma, supongamos el siguiente ejemplo.
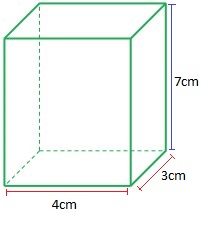
El área de la base se resuelve multiplicando 4cm por 3cm, como también tenemos que tener en cuenta el techo, entonces tenemos que multiplicar el resultado por dos.
- Area de la base = (4cm * 3cm) * 2
- = 24 cm
Ahora tenemos que hacer lo mismo pero con los laterales, en este ejemplo deberíamos multiplicar 3cm * 7cm, pero como tenemos 4 caras laterales idénticas ese resultado tendríamos que multiplicarlo por 4.
- Area de las caras laterales = (3cm * 7cm) * 4
- = 84cm
Lo siguiente es simple, tenemos que sumarizar las áreas anteriormente calculadas para obtener el área total de nuestro prisma rectangular.
- Area total = 24cm + 84cm
- = 108cm
En resumen, podemos calcular el área de un prisma rectangular mediante la siguiente formula.
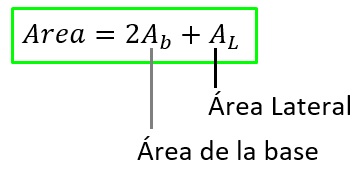
Sigamos practicando, veamos el siguiente ejemplo.
PRIMER EJEMPLO
Tenemos la misma figura del ejemplo anterior pero con diferentes medidas, veamos que aplicando la ultima formula obtenemos el área rápidamente.
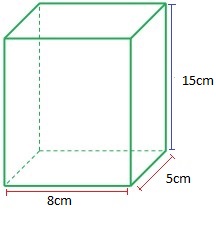
- Area total = 2(8cm * 5cm) + 4(5cm*15cm)
- = 80cm + 300cm
- = 380cm
SEGUNDO EJEMPLO
(un poco mas difícil 🙂 )
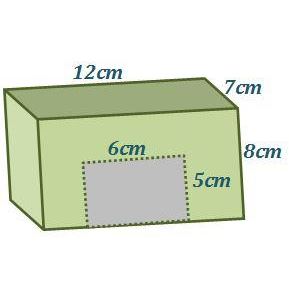
Supongamos que tenemos el siguiente prisma rectangular, que bien podríamos pensarlo como una jaula, y nos piden que calculemos el área de toda la superficie sin incluir la puerta (rectángulo gris de la figura). Además, imaginemos que sólo está tapada por la parte superior de la misma (no posee un suelo ya que al estar apoyada no lo necesita).
Entonces, si necesitamos pintar toda la jaula sacando su puerta, ¿cómo se podría calcular cuánto material necesitaremos para cubrirla?

Cómo sabemos que esta jaula no posee un piso y tampoco debemos tomar en cuenta la puerta, siguiendo los lineamientos de los conceptos mencionados anteriormente, el calculo quedaría de la siguiente manera.
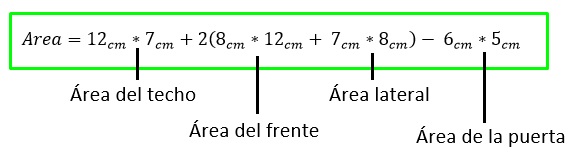
Luego, al realizar los cálculos nos queda el siguiente resultado.

Y así es como podemos utilizar la fórmula original en caso de que sea un prisma rectangular convencional o también cómo podemos adaptar esta para que pueda ser de utilidad en caso de problemas dónde debemos quitar o restar ciertas partes del prisma.
CÓMO CALCULAR EL VOLUMEN DE UN PRISMA
Entendemos por volumen la medida del espacio ocupado por un cuerpo de tres dimensiones, vamos a calcular el volumen del siguiente prisma.
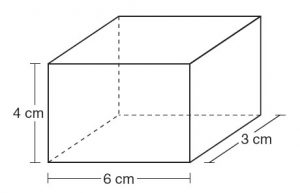
PRIMER EJEMPLO
En el caso del volumen, la fórmula es incluso más fácil. Simplemente tenemos que calcular el area de la base y multiplicarla por la altura.
- Volumen = (6cm * 3cm) *4cm
- 72cm3
La unidad el Volumen es en unidades cubicas, dado que es un sistema tridimensional, en este caso como lo estamos haciendo en centímetros el resultado debe estar en centímetros cúbicos.
"Es importante que siempre escribas las unidades de volumen en el resultado"
EJEMPLO 2
Muchas veces nos puede pasar que queremos conocer el volumen que ocupará un objeto que vamos a adquirir, ya sea un ropero, un escritorio, una mesa, etc. Esto se calculará de la misma manera en la que venimos haciendo hasta ahora.
Imaginemos que vamos a comprar una mesa que tiene las siguientes medidas:
- Longitud: 173 cm
- Ancho: 90 cm
- Altura: 78 cm

Ahora, simplemente debemos de reemplazar los datos en nuestra formula que vimos anteriormente. Que nos quedará de la siguiente manera.

Espero que con estos ejemplos que comentamos te quede claro el la idea y la metodología de resolución de los problemas, te quiero invitar a que revises lo siguientes artículos, puede ser de ayuda para seguir aprendiendo. 🙂
También quiero compartirte el siguiente vídeo, de Khan Academy, que sin dudas puede ser de gran ayuda 🙂
¡Si te fue de utilidad el artículo no dudes en dejarme tus cinco estrellas aqui debajo 🙂 !
Si quieres conocer otros artículos parecidos a CÓMO CALCULAR EL ÁREA Y EL VOLUMEN DE UN PRISMA RECTANGULAR puedes visitar la categoría Matemática.
-
-
Hola, creo que hay un error en la primera demostración porque multiplicaste 4*3*7, y debe ser 2*4*7 3*4*7 porque en los laterales todos tienen la misma altura pero no todos tienen el mismo ancho de base hay lados con un ancho de base igual a 3 y otros igual a 4. Lo mismo ocurre con el primer ejemplo: no debe ser 4*5*15 sino que hay dos que son 8*5*15
-
Error en ejercicio de "caras laterales" del primer ejemplo: se aplica (3*7)*4 pero debería ser (3*7)*2 + (4*7)*2, ya que hoy dos medidas diferentes en los anchos de las latrales (3 y 4 cm) pero la altura no varía (7cm).
Deja un comentario
En el primer ejemplo de Volumen el resultado es en cm^3 no cm^2, por lo demás esta bien.