Cómo calcular el área de un círculo
Para calcular el área de un círculo necesitas saber el radio o el diámetro, es decir la distancia que existe desde el centro de la circunferencia hasta el borde, luego aplicar la siguiente formula (A = Π x r²)
Para que quede todo mas claro y poder explicar los conceptos teóricos antes mencionados vamos con un ejemplo practico.
¡Te puede interesar! 👉 cómo calcular el área de un triangulo
1️⃣ Ejemplo 1
Cómo calcular el área de un círculo con diámetro
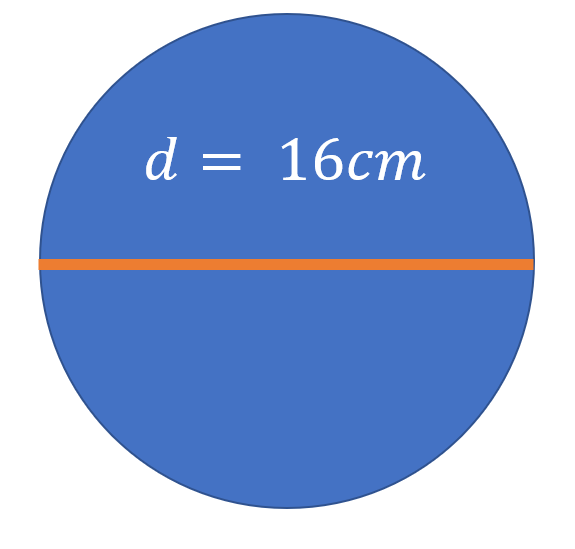
Calcular el área de un círculo cuyo diámetro es de 16cm.

Bien, como dijimos al comienzo, necesitamos conocer el radio, pero en su lugar el enunciado nos entrega el diámetro, que es el doble del radio, con lo cual el r = d/2 = 8cm
Ahora, solo nos queda aplicar la formula A = Π x r² quedando de la siguiente manera.
A = Π x r²
A = Π x (8cm)²
A = Π x (8cm)² = Π x 64cm² = 200,96 cm²
Y el resultado es que el área del círculo es de 200.96 centímetros cuadrados
2️⃣ Ejemplo 2
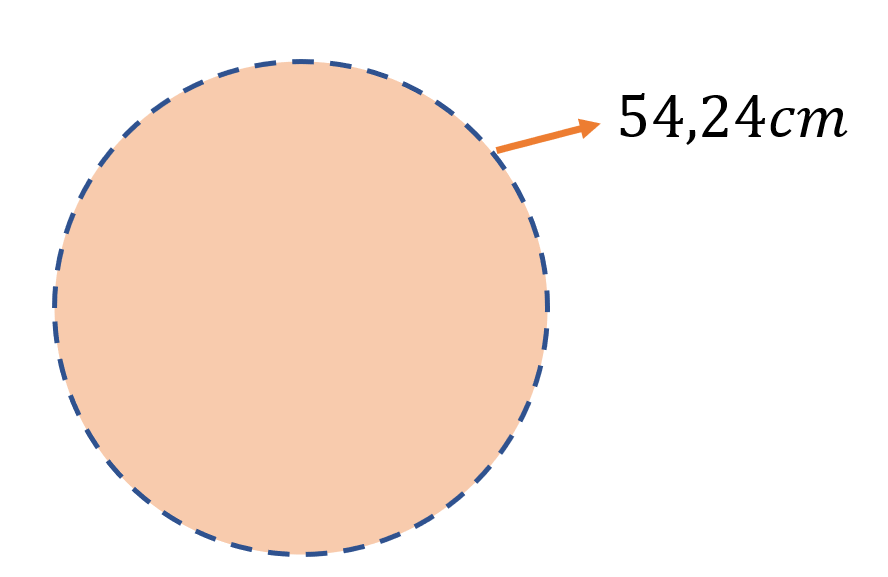
Cómo calcular el área de un circulo con el perímetro
Lo primero, es saber la relación que existe entre el perímetro y el radio, no esta de mas comentar que el perímetro de una circunferencia es la longitud, y se relaciona con el diámetro a través de la siguiente formula.
perímetro = 2Πr (dos pi por radio)
con lo cual, despejando nos queda que el radio es r = perímetro/ 2Π
al reemplazar los valores del enunciado nos queda r = 54,24/ 2x3,14 = 8cm
Ahora que ya conocemos el radio, tenemos que aplicar la formula del ejemplo 1
A = Π x r²
A = Π x (8cm)²
A = Π x (8cm)² = Π x 64cm² = 200,96 cm²
Como seguramente ya te diste cuenta, calcular el área de un circulo es muy simple, dado que solo necesitamos el dato del radio, y si no lo tenemos es cuestión de conocer la relación entre el dato que nos dan en el enunciado para hallarlo.
Si quieres conocer otros artículos parecidos a Cómo calcular el área de un círculo puedes visitar la categoría Matemática básica.
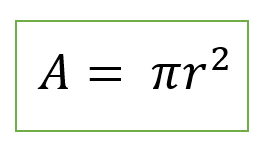


Deja un comentario