
CHOQUE ELÁSTICO E INELÁSTICO - EJERCICIOS RESUELTOS

Como vimos en un articulo anterior (choque elástico e inelástico), un choque de dos cuerpos o mas lo podemos categorizar de dos maneras, o es un choque elástico o inelástico.
- En un choque elástico tanto la energía como la cantidad de movimiento antes y después del choque se conservan, es decir que no se producen perdidas de energía en deformaciones.
- En un choque inelástico los dos cuerpos después del choque forman uno solo, es decir que ambos se mueven juntos a la misma velocidad.
EJERCICIOS RESUELTOS
A continuación vamos a ejemplificar la teoría con algunos ejercicios resuelto, si no leyó el primer articulo teórico le invitamos a visitar el siguiente enlace ver teoría
EJERCICIOS 1
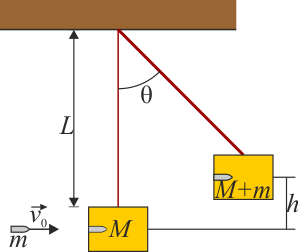
Un péndulo balístico, es un objeto utilizado para medir la velocidad de la bala midiendo el angulo que imprime esta al colisionar con el péndulo.
Observemos la siguiente imagen, la bala es disparada hacia el bloque que inicialmente se encuentra en reposo, luego de la colisión todo el sistema se mueve un determinado angulo en dirección del impacto, despues del choque tanto la bala como el bloque se mueven a la misma velocidad, dado que esta queda en e interior del bloque, si suponemos que no hubo perdida de energía en factores externos (color, deformaciones, etc), podemos considerar que es un choque perfectamente inelástico.
ENUNCIADO
Una bala de 10 gramos choca contra un péndulo balístico de 2 kilos, en la primera oscilación el péndulo se eleva 16 cm.
1 - Calcular la velocidad de la bala antes del impacto.
2 - Calcular la energía cinética de la bala antes del choque.
RESOLUCIÓN
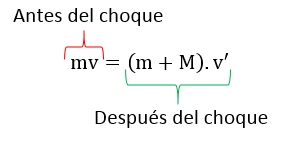
Dado que consideramos que no existe perdida de energía en el impacto y que la cantidad de movimiento se conserva podemos establecer la siguiente relación.
Donde m representa la masa de la bala y M la masa del bloque, v representa la velocidad de la bala antes del impacto y v' la velocidad del conjunto después del impacto, esta velocidad es la velocidad tangencial del movimiento pendular.
Ahora, con esto no es suficiente, necesitamos encontrar una ecuación mas, sabemos que si la cantidad de movimiento se conserva, también lo hace la energía del sistema, con lo cual podemos pensar el asunto como una relación de energías iniciales y finales.
[anuncio_b30 id=3]
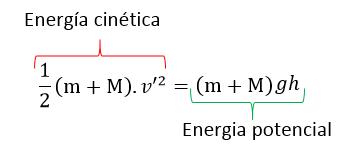
Dicho esto podemos pensar la siguiente igualdad, inmediatamente después del choque la relación de energía es la siguiente.
Al relacionar estas dos ecuaciones, llegamos a que la velocidad del bloque inmediatamente después del choque es la siguiente.
Ahora al relacionar la velocidad final con la inicial obtenemos la siguiente ecuación, y ahí ya podemos reemplazar los valores para obtener el resultado.
Ahora que sabemos cuando es la velocidad que trae la bala podemos calcular su energía cinética en el estadio inicial.
EJERCICIO 2
ENUNCIADO
Un cuerpo de masa m = 4kg se mueve según una recta con velocidad de 6 m/s. Delante de el marcha otro de 6kg, con velocidad de 3 m/s, en el mismo sentido. siendo el choque plástico determinar
1 - la velocidad de ambos después del choque.
2 - La energía cinética perdida en el choque.
RESOLUCIÓN
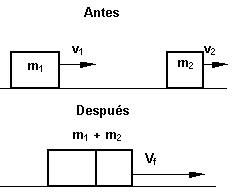
El enunciado nos dice, que el choque es plástico, lo que quiere decir que los dos cuerpos continúan unidos luego del choque.
Como sabemos que la cantidad de movimiento en cualquier choque es conservativa podemos plantear las siguientes ecuaciones.
Reemplazando los datos obtenemos como resultado que la velocidad final del conjunto es 4,2 m/s.
"DESPUÉS DE UN CHOQUE PLÁSTICO, LOS DOS CUERPOS QUEDAN UNIDOS Y SE MUEVEN A LA MISMA VELOCIDAD"
Para calcular la energía perdida por el impacto solo tenemos que calcular la energía de cada cuerpo antes del impacto y compararla con la energía del conjunto luego del impacto.
La energía tanto antes como después del impacto es totalmente cinética, dado que los cuerpos están en movimiento pero en el suelo y no tienen energía potencia.
[anuncio_b30 id=3]
Reemplazando los valores en la formula obtenemos que como resultado del impacto, la perdida de energía fue de aproximadamente 10,8J.
EJERCICIO 3
ENUNCIADO
Una esfera de 2KG se mueve hacia la derecha a una velocidad de 5 m/s y choca contra otra de 3KG que se mueve a 2 m/s en igual dirección y sentido. Despues del choque la esfera de 3Kg se mueve a 4,2 m/s. Determinar.
1 - La velocidad de la otra esfera después del choque.
2 - El coeficiente de restitución K.
RESOLUCIÓN
Como siempre decimos, el impulso es conservativo en cualquier choque con lo cual siempre podemos plantear la siguiente ecuacion.
De la ecuacion solo tenemos que despejar v1' que representa la velocidad del cuerpo 1 después del choque, si despejamos y reemplazamos los valores obtenemos como resultado lo siguiente.
Ahora tenemos que calcular el coeficiente de restitución, pero antes de calcularlo tenemos que comentar que el coeficiente de restitución es un coeficiente mayor a cero y menor que uno que indica una relación entre las velocidades de los cuerpos antes del choque con las velocidades de dichos cuerpos después del choque.
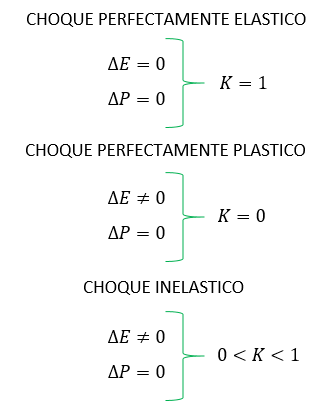
Cuando el Coeficiente de restitución K es igual a 1, eso quiere decir que no existe perdida de energía en el choque (Choque perfectamente elástico), cuando el coeficiente es igual a 0, significa que existe perdida de energía en el choque y que el choque es (perfectamente plástico).
Cuando el coeficiente es mayor que cero y menor que uno significa que existe perdida de energía en el impacto y que el choque es inelastico (no es ni perfectamente plástico ni perfectamente elástico)
La siguiente formula es la que nos permite calcular el coeficiente y según su resultado ya podemos catalogar el tipo de choque ocurrido.
Al reemplazar los valores de las velocidades de nuestro ejercicio obtenemos como resultado lo siguiente.
Próximamente vamos a estar subiendo mas ejercicios y ejemplo de la misma temática, pero en dos dimensiones, les invito a dejar sus comentarios y sugerencias. 🙂
Si quieres conocer otros artículos parecidos a CHOQUE ELÁSTICO E INELÁSTICO - EJERCICIOS RESUELTOS puedes visitar la categoría Fisica.
-
-
En el ejercicio numero 2 el numeral "b" están preguntando la energía perdida, no el cambio de energía.
-
Tengo este problema. Cómo lo resuelvo? Dos automóviles exactamente iguales chocan de frente. Te presentamos tres casos: a) Los dos venían a 40 Km/h cada uno.
b) Unoveníaa60Km/hyelotroa20Km/h.
c) Uno venía a 80 Km/h y el otro estaba detenido.
¿En cuál de los tres casos son peores los daños? ¿O son iguales en todos los casos? -
5. Un bloque A de 4 kg se mueve con una velocidad de 10 𝑗⃗ m/s y choca frontalmente con un bloque B de 1 kg, si luego del choque el bloque A queda en reposo determinar la velocidad que tenía el bloque B antes del choque.
a) El choque es perfectamente elástico
b) El choque es perfectamente inelástico -
En el segundo problema, los móviles se desplazan en el mismo sentido, con lo que la velocidad a la que chocan es la velocidad relativa de uno respecto al otro, y no la velocidad inicial de cada uno, como se expone en su solución.
Deja un comentario
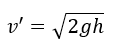
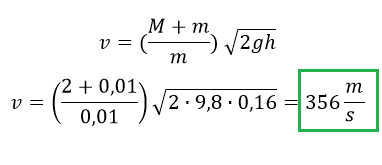
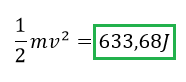
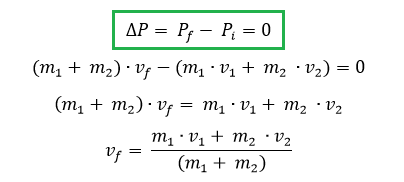
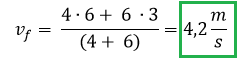
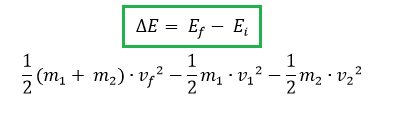
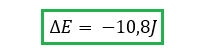
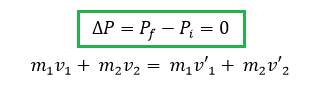
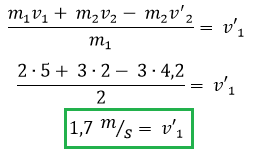
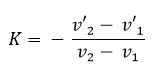






muy buenos ejercicios que ayudan a los chicos que necesitan mejorar sus conocimientos , asi mismo a los docentes . gracias Oscar