MÉTODO DE SUSTITUCIÓN
El Método de Sustitución es uno de los métodos mas utilizados para resolver sistemas de ecuaciones lineales, con este método se pueden resolver cualquier sistema de ecuaciones, aunque resolver un sistema de mas de 3 incógnitas, es decir mas de 3x3 ya seria muy laborioso.
Entonces, antes de usar este método lo primero que tenemos que saber es si es un sistema lineal, pero ¿que es un sistema linea? veamos eso.
¿QUE ES UNA ECUACIÓN LINEAL?
Para que un sistema de ecuaciones sea considerado linea, todas las ecuaciones de nuestro sistema tiene que ser de primer grado, es decir que la X no tenga un exponente mayor que uno.
Luego de verificar que todas las ecuaciones sean de primer grado, vamos al método de resolución.
Como lo dice el nombre, es un método, y como todo método hay que seguir una receta paso a paso, a continuación el orden de las acciones que tenemos que realizar.
[anuncio_b30 id=3]
MÉTODO DE SUSTITUCIÓN PASO A PASO
Este método aplica para sistemas de ecuaciones de cualquier dimensión, es decir 2x2, 3x3 ... NxN, pero a modo practico voy a enunciarlo pensando en un sistema de de 2x2.
- Elegir una ecuación y despejar una de sus incógnitas (puede ser cualquiera).
- Remplazar en la otra ecuación la incógnita despejada en el primer paso
- Ahora nos queda una ecuación de una sola incógnita, despejar la incógnita (el resultado debe ser un numero)
- Reemplazar el resultado del paso 3 en cualquiera de las dos ecuaciones y despejar la incógnita.
Dicho esto, no damos mas vueltas y vamos a ver ejercicios resueltos con dos incógnitas.
EJERCICIOS RESUELTOS
Vamos a ver dos ejemplos, donde mostrare paso a paso como utilizar el método para llegar al resultado, luego al final vamos a repasar cada uno de los pasos.
EJEMPLO 1
Supongamos que tenemos que resolver el siguiente sistema de ecuaciones, ya se puede ver que es un sistema lineal (importante) y dicho esto procedemos a la resolución.
Lo primero que tenemos que hacer es elegir una ecuación y despejar cualquier incógnita, yo voy a elegir la primera y despejar X simplemente por que en este caso es lo mas fácil. 🙂
Al despejar la primera ecuación, muuuuuyyyy fácil, obtenemos lo siguiente (en verde), la ecuación despejada.
Lo segundo, tenemos que colocar la variable despejada en la ecuación elegida, en la otra ecuación, haciendo esto obtenemos lo siguiente.
Ahí, te das cuenta que ya podemos resolver esa ecuación por que todo quedo en función de y, entonces lo tercero que tenemos que hacer es despejar Y, abajo el paso a paso del despeje.
Ahora ya sabemos cual es el valor de Y, lo cuarto que tenemos que hacer es lo mas simple, reemplazamos ese valor encontrado Y = -1 en cualquiera de las dos ecuaciones.
Yo elegí la primera simplemente por que es mas fácil 🙂
EJEMPLO 2
Este ejemplo lo quiero dar por que su resultado es un caso particular, que seguramente va a ser de utilidad para entender los resultados obtenidos.
Supongamos un sistema de ecuaciones como el siguiente (seguro ya te diste cuenta que la primer ecuación es la misma que el ejemplo anterior), es a propósito 🙂
Lo primero, despejo X de la primera ecuación (lo mismo que hicimos antes) 🙂
Lo segundo, tenemos que colocar la variable despejada en la ecuación elegida, en la otra ecuación, haciendo esto obtenemos lo siguiente.
Lo tercero, despejar Y. a ver que pasa.
Lo cuarto, como hicimos antes, es reemplazar el valor obtenido( y = 0) en cualquiera de las ecuaciones anteriores, entonces reemplazando obtenemos lo siguiente.
CONCLUSIONES
Simplemente hay que respetar paso a paso el método que nombre al comienzo, los volvemos a repasar 🙂
- Elegir una ecuación y despejar una de sus incógnitas (puede ser cualquiera).
- Remplazar en la otra ecuación la incógnita despejada en el primer paso
- Ahora nos queda una ecuación de una sola incógnita, despejar la incógnita (el resultado debe ser un numero)
- Reemplazar el resultado del paso 3 en cualquiera de las dos ecuaciones y despejar la incógnita.
Obviamente, en matemática existen muchas formas de hacer lo mismo, existen varios métodos de resolución de ecuaciones, el método de sustitución no es el único, existe el método de igualación o el metodo de determinantes, en fin podemos utilizar el método que mas fácil nos resulte 🙂
Si todo esto te pareció poco, o no te quedo del todo claro, te invito a que te mires completo el siguiente vídeo, donde se explica claramente mediante un ejemplo todo lo que aquí les comente. 🙂
REFERENCIAS
- https://es.khanacademy.org
Si quieres conocer otros artículos parecidos a MÉTODO DE SUSTITUCIÓN puedes visitar la categoría Matemática.
-
Siendo sincera no entendi nada, falta explicar mejor, pero gracias por el servicio
Deja un comentario
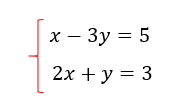
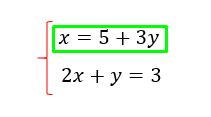
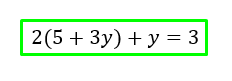
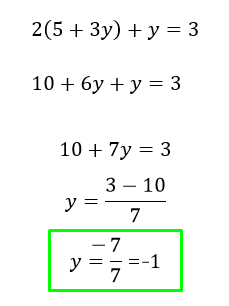
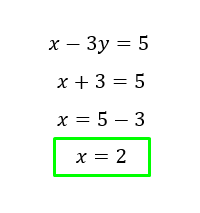
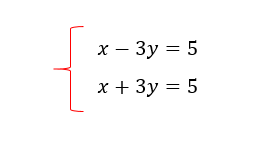

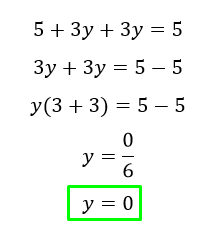
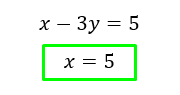
ME PODRIAN DAR OTRO EJEMPLO POR FAVOR.
GRACIAS.