
HIDRODINÁMICA

Un fluido es un sistema material cuyas moléculas se mueven libremente unas con respecto a las otras. Los líquidos y los gases son fluidos. En este artículo vamos a ocuparnos de la dinámica de los líquidos (fluidos incomprensibles, es decir, que mantienen constante su volumen al comprimirlos), con las limitaciones siguientes: trataremos los líquidos no viscosos (que se mueven sin pérdida de energía) y en el régimen laminar, no turbulento (en que no se cortan los caminos que siguen las diferentes partículas, sin remolinos) Supondremos además que a lo largo del camino no hay ni fuentes ni sumideros, por lo que se conservará la masa total del líquido.
Teorema de Bernoulli
Con una enorme cantidad de partículas en movimiento, es imposible ocuparnos de las características de cada una de ellas. Sin embargo, podemos estudiar la energía total del conjunto e imponer la condición de que se conserve: cualquier variación de energía será debida al trabajo realizado por alguna fuerza exterior. Como también se conserva la masa y el fluido es incompresible, el volumen V del líquido que atraviesa dos secciones del tubo de corriente en el mismo tiempo es idéntico. Por ello, el liquido ira más deprisa en los pasos estrechos.
¿Qué fuerza actúan sobre un liquido que se mueve? Aparte de su propio peso, existen las presiones a que lo someten el tubo, la atmósfera o cualquier otro agente externo. Así pues, la energía de cualquier parte del liquido solo puede variar a causa de un cambio de velocidad v (energía cinética), del nivel geográfico o altura h (energía potencial gravitatoria), o de la presión p (trabajo externo). La suma de los tres términos debe ser constante en cualquier punto e instante.
Los dos volúmenes de líquidos V1 y V2 son iguales, puesto que son los que han atravesado las dos secciones en el mismo tiempo. La variación de energía cinética que experimenta el liquido al pasar de la primera zona a la segunda es debida a los trabajos efectuados por su peso y por la presión a que esta sometido.
Para la unidad de volumen se cumplirá siendo d = m/V la densidad del liquido, p+d.v2/2 + d.g.g = cte, que es una de las formas de expresar el teorema de Bernoulli, que es considerado como el principio fundamental de la hidrodinámica.
Efecto Venturi
Si el fluido circula horizontalmente y, por lo tanto, el nivel es constante, la suma de los dos primeros términos de la ecuación de Bernoulli debe permanecer constante. Toda la variación de velocidad (por ejemplo, al cambiar la sección del tubo) comporta una variación en la presión del fluido, lo que es conocido como el efecto Venturi.
Muchas son las aplicaciones de este efecto; entre ellas, alguna tan viciosa como elevar un papel sujeto por un extremo, al sopar por encima de él. Muy habitual es el uso de los pulverizadores, tanto en perfumería como en los carburadores de los motores de explosión; en ellos, succiona por depresión el líquido, obligándolo a ascender y ponerse en medio de la corriente y ser así pulverizado. En el caso de una pelota lanzada con efecto, en el aire (cuya velocidad es diferente con un lado y otro de la pelota) el que tuerce su camino, en forma semejante a como sostiene un avión en vuelo gracias a la forma de sus alas.
El efecto Venturi es también la base del funcionamiento de las trompas de vacío, usadas en los laboratorios, y de algunos aparatos que se emplean para medir la velocidad de vuelo de los aviones.
Teorema de Torricelli
En un deposito con salida, el desagüe tiene una sección mucho menos que la superficie libre del liquido, por lo cual, al desaguar, la velocidad del liquido en la parte superior del depósito es despreciable con respecto a la velocidad de salida. Si aplicamos el teorema de Bernoulli a este gas (observando que la presión exterior sobre ambas superficies libres es la atmósfera), se comprueba que la energía potencial que desaparece arriba es igual a la energía cinética que aparece abajo. A la misma conclusión se llega si imaginamos la sustitución del liquido de abajo por el correspondiente de arriba con el resto inmóvil (como en la imagen que se muestra a continuación).
Así, la velocidad de salida del agua por el agujero es la misma con que caería desde arriba del depósito.
Viscosidad
En los líquidos reales hay que tener en cuenta la pérdida de energía debida a la acción de las fuerzas que se oponen al desplazamiento relativo de las distintas partes del líquido entre sí. Este rozamiento interno de los líquidos se mide mediante el coeficiente de viscosidad, que es propio de cada sustancia y suele depender de la temperatura.
¿Qué te pareció este artículo? ¡No olvides dejarnos tu comentario aquí abajo ante cualquier consulta!
Si quieres conocer otros artículos parecidos a HIDRODINÁMICA puedes visitar la categoría Fisica.


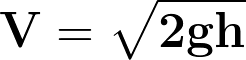





Deja un comentario