
PUNTO DE INTERSECCIÓN ENTRE DOS RECTAS
Cuando analizamos el comportamiento de dos rectas en el eje cartesiano puede existir tres resultados posibles, que se corten en un único punto, que no se corten nunca o que estén una sobre la otra, es decir que sea la misma recta. Si las rectas no se cortan nunca entre si decimos que esas dos rectas son paralelas. La idea de este articulo es estudiar el caso donde las dos rectas se cortan en un único punto.
VEAMOS UN EJEMPLO
Supongamos que tenemos que encontrar el punto de intersección de las siguientes dos rectas "si es que existe" y tenemos que graficarlo en el eje cartesiano.
Para encontrar el punto de intersección tenemos que pensar estas dos rectas como si fueran un sistema de ecuaciones, podemos utilizar cualquier método de resolución para resolverlo, en este ejemplo vamos a utilizar el método de igualación.
Al igualar las dos ecuaciones, pudimos despejar el valor de X, ahora simplemente reemplazando ese valor en cualquiera de las dos ecuaciones obtendremos el valor de Y.
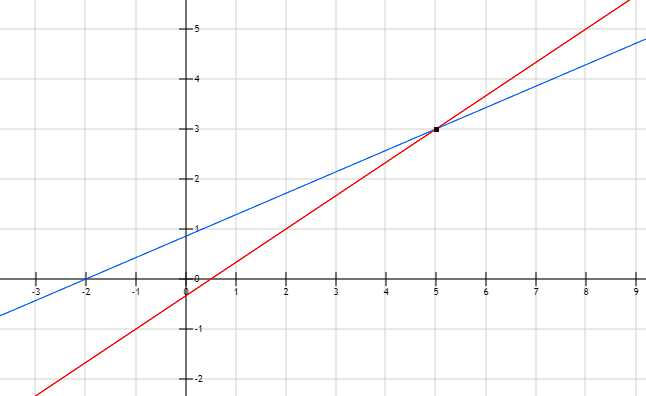
Ahora que tenemos esta información, podemos afirmar que las dos rectas se cruzan en el punto (5,3), pero para que no quede ningún tipo de dudas vamos a graficarlas y verificar el resultado.
Como podemos confirmar en la gráfica, las rectas efectivamente se cruzan en el punto (5,3).
[anuncio_b30 id=3][anuncio_b30 id=4]
CONCLUSIÓN
- Lo primero que tenemos que hacer es igualar las dos rectas.
- Luego despejamos el valor de X.
- Una ves que ya tenemos el valor de X, despejamos el valor de Y. Ya tenemos el punto de intersección.
- Para que no quede ninguna duda, podemos graficar las dos rectas.
Es importante entender, que no siempre dos rectas se van a cortar, en el caso de las rectas paralelas por ejemplo que no se cortan nunca, al igualar las dos ecuaciones nos quedara un sistema incompatible (no tiene solución), eso nos quiere decir que no hay punto de intersección entre ambas rectas.
Si quieres conocer otros artículos parecidos a PUNTO DE INTERSECCIÓN ENTRE DOS RECTAS puedes visitar la categoría Matemática básica.
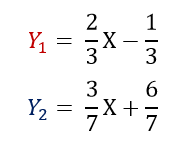
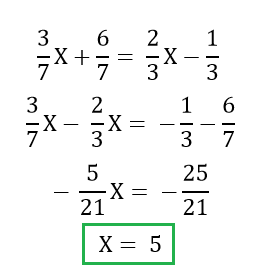
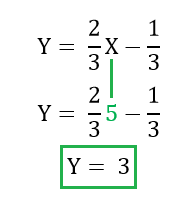


Deja un comentario