
SUPERPOSICIÓN DE FUERZAS
Principalmente, te invitamos a leer nuestro artículo sobre fuerzas e interacciones para entrar en tema sobre lo que viene a continuación.
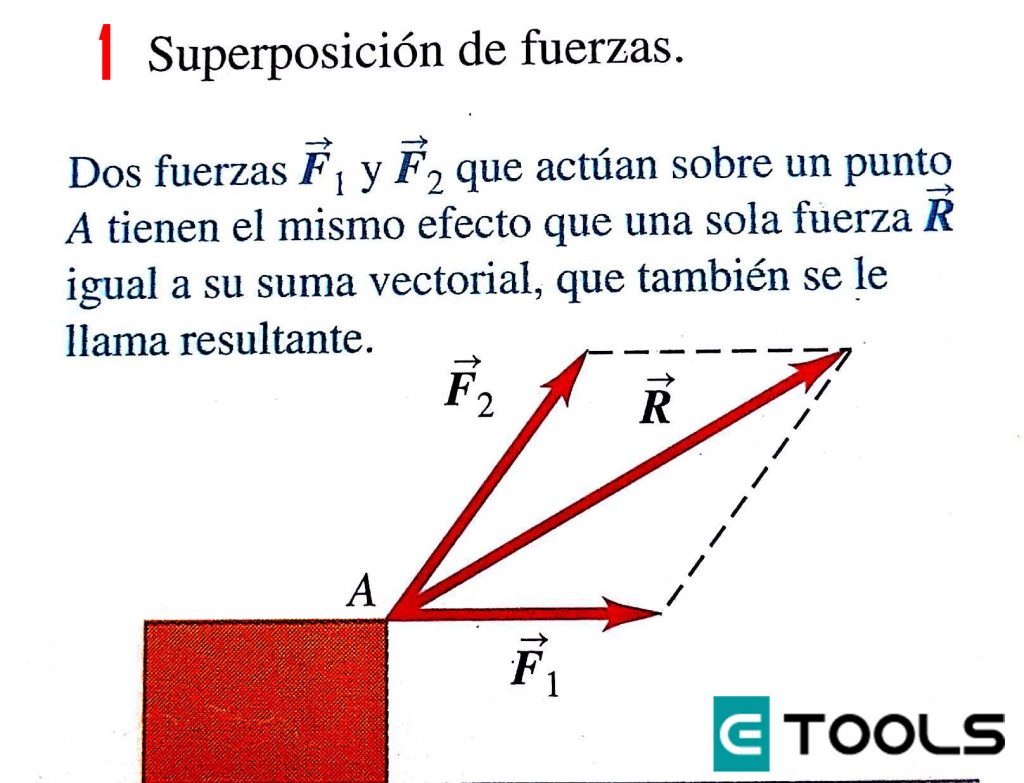
Cuando se lanza una pelota, hay al menos dos fuerzas que actúan sobre ella, el empujón de la mano y el tirón hacia debajo de la gravedad. Los experimentos muestran que si dos fuerzas y actúan al mismo tiempo en un punto A de un cuerpo (imagen 1), el efecto sobre el movimiento del cuerpo es igual al de una sola fuerza igual a la suma vectorial de las fuerzas originales.
En general, el efecto de cualquier cantidad de fuerzas aplicadas a un punto de un cuerpo es el mismo de una sola fuerza igual a la suma vectorial de las fuerzas. Éste es el importante principio de superposición de las fuerzas.
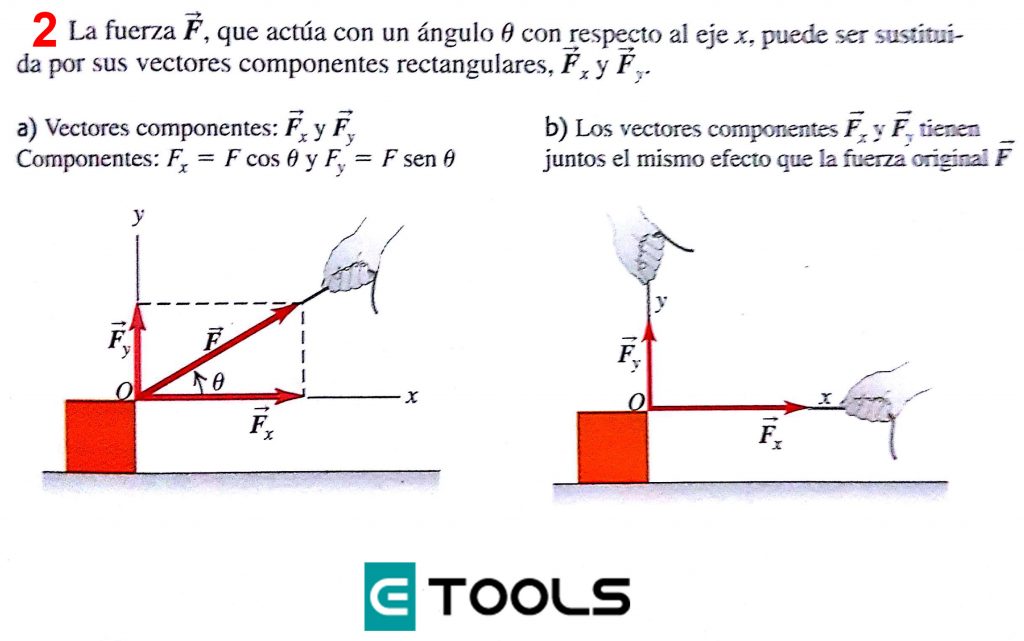
El descubrimiento experimental de que las fuerzas se combinan por suma vectorial es de enorme importancia. Usaremos este hecho muchas veces es nuestro estudio de la física, pues nos permite sustituir una fuerza por sus vectores componentes. Por ejemplo, en la imagen que tenemos a continuación (2A), la fuerza actúa sobre un cuerpo en el punto 0. Los vectores componentes de en las direcciones y son y . Si éstos se aplican simultáneamente, como en la figura (2B), el efecto es idéntico a la fuerza original . Cualquier fuerza puede ser sustituida por sus vectores componentes, actuando al mismo tiempo.
Suele ser más conveniente describir una fuerza en términos de sus componentes x y y, y en vez de sus vectores componentes. En el caso de la figura (2) y son ambas positivas; para otras orientaciones de , cualquiera puede ser negativa o cero.
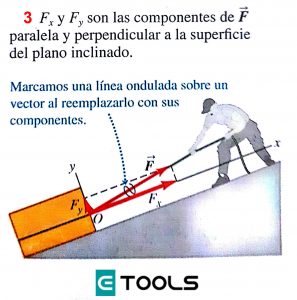
Ninguna regla establece que los ejes de coordenadas deben ser verticales y horizontales, en la figura (3) un bloque de piedra es arrastrado rampa arriba por una fuerza , representada por sus componentes y , paralela y perpendicularmente a la rampa inclinada.
A menudo necesitaremos obtener la suma vectorial (resultante) de todas las fuerzas que actúan sobre un cuerpo. Llamaremos a esto la fuerza neta que actúa sobre el cuerpo. Usaremos la legra griega ∑ para detonar sumatoria. Si las fuerzas son , etcétera, abreviaremos la sumatoria como:
Dónde se lee “suma vectorial de las fuerzas” o “fuerza neta”. La versión con componentes de la ecuación (4.1) es el par de ecuaciones:
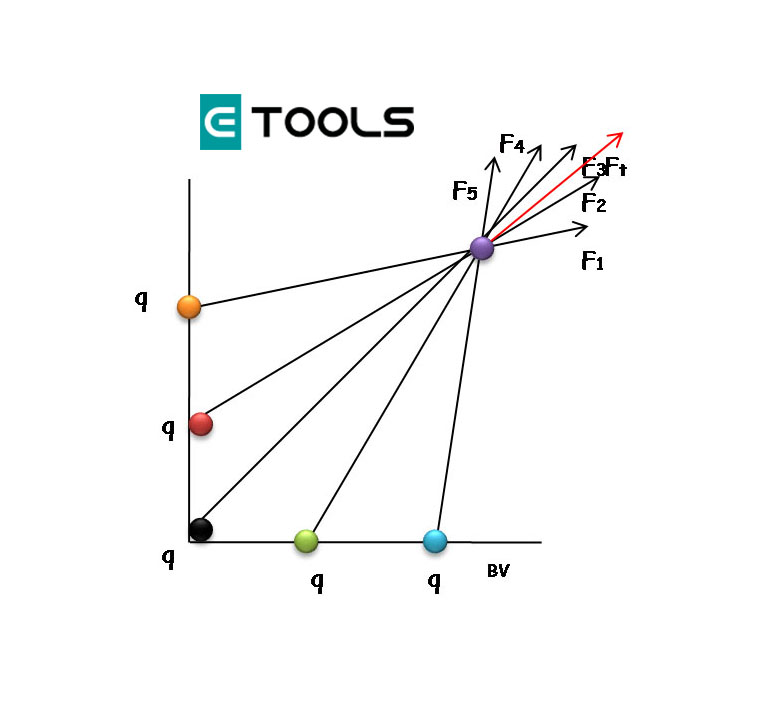
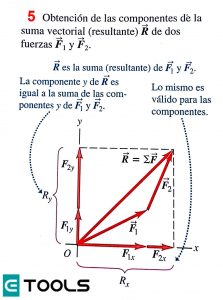
Dónde ∑ es la suma de componentes X y ∑ es la suma de componentes Y, como en la imagen (5). Cada componente puede ser positiva o negativa, así que tenga cuidado con los signos al sumar en la ecuación (4.2)
Una vez que se tienen y , puede obtenerse la magnitud y la dirección de la fuerza neta que actúa sobre el cuerpo. La magnitud es:
Y el ángulo θ entre y el eje +x puede obtenerse la relación tanθ = / . Las componentes y pueden ser positivas, negativas o cero. Y el ángulo θ puede estar en cualquier cuadrante.
En problemas tridimensionales, las fuerzas pueden tener componentes Z, así que agregamos a la ecuación de la magnitud neta lo siguiente:
No olvides que puedes visitar nuestro anterior artículo sobre fuerza e interacciones para entrar en el tema.
Si quieres conocer otros artículos parecidos a SUPERPOSICIÓN DE FUERZAS puedes visitar la categoría Fisica.
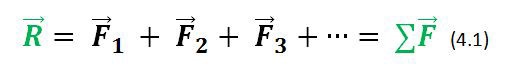








Deja un comentario