
IMPULSO Y CANTIDAD DE MOVIMIENTO

DEFINICION DE IMPULSO Y CANTIDAD DE MOVIMIENTO
Cuando hablamos de impulso y cantidad de movimiento siempre surgen algunas dudas, por eso es importante tener clara la definición. 👇
Por definición, el impulso es el producto de la fuerza aplicada sobre un cuerpo y el tiempo de duración, supongamos el siguiente ejemplo, un padre le da un impulso a su hija que se encuentra en el columpio de una plaza.
El impulso será la intensidad de la fuerza aplicada por el tiempo de duración de la misma.
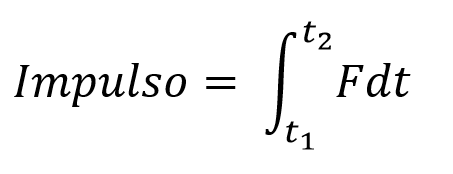
La cantidad de movimiento, es un resultado del impulso, aunque matemáticamente son lo mismo, conceptualmente existen diferencias.

RELACIÓN ENTRE IMPULSO Y CANTIDAD DE MOVIMIENTO
Como dije antes, tanto el impulso como la cantidad de movimiento están relacionados mediante la siguiente igualdad.
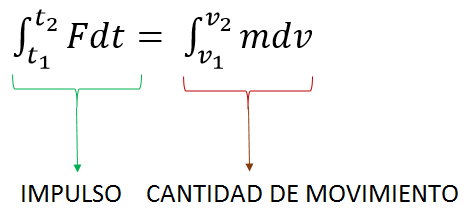
Naturalmente, la integral del impulso solo se puede calcular si se conoce la fuerza en función del tiempo, sin embargo, la integral del segundo miembro conduce siempre al siguiente resultado.
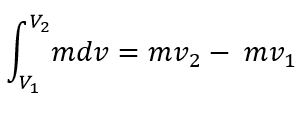
El producto de la masa de una partícula por su velocidad se denomina cantidad de movimiento de la partícula, y es también una magnitud vectorial.
La ecuación de impulso (el primer miembro) expresa el siguiente hecho importante
La principal aplicación de este teorema se relaciona con las fuerzas de corta duración, tales como las originadas en choques o explosiones.
En cualquier sistema, la unidad de impulsión e igual al producto de las unidades de fuerza y tiempo de dicho sistema.
La impulsión de cualquier componente o fuerza cuya dirección es constante, suele representarse graficamente llevando los tiempos en abscisas, y las fuerzas en ordenadas. El área comprendida debajo de la curva, entre las coordenadas correspondientes a t1 y t2, es igual a la impulsión de la fuerza durante ese intervalo.
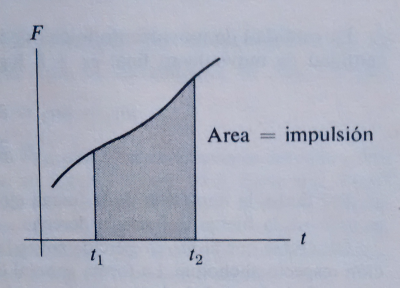
Si la impulsión de una fuerza es positiva, la cantidad de movimiento del cuerpo sobre el cual actúa aumenta algebraicamente, y si es negativa disminuye. Si a impulsión es nula, no hay variación de la cantidad de movimiento.
CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO
Siempre que exista una fuerza de interacción entre dos partículas, la cantidad de movimiento de cada una se modifica como resultado de la fuerza que la otra ejerce sobre ella.(la fuerza puede ser gravitatoria, magnética, eléctrica o de cualquier otro origen)
Además, dado que por la tercera ley de newton, la fuerza sobre una de las partículas es siempre de igual magnitud y sentido opuesto a la de la otra, las correspondientes impulsiones son también de igual magnitud y sentido opuesto.
De ello se deduce que el vector incremento de la cantidad de movimiento e cada particula, durante un intervalo de tiempo cualquiera, es de igual magnitud y sentido opuesto que el vector incremento de la cantidad de movimiento de la otra.
El incremento neto de la cantidad de movimiento del sistema (conjunto de ambas partículas) es , por lo tanto, nulo.
La pareja de fuerzas de acción y reacción esta formado por fuerzas interiores al sistema, y de ello deducimos que la cantidad de movimiento total de un sistema de cuerpos no puede modificarse por las fuerzas interiores ejercidas sobre ellos.
Por lo tanto, si las únicas fuerzas que actúan sobre las partículas de un sistema son las fuerzas interiores, la cantidad de movimiento permanece constante tanto en magnitud como en sentido.
El principio de la cantidad de movimiento se enuncia de la siguiente manera.
El principio de conservación de la cantidad de movimiento es uno de los mas fundamentales e importantes de la mecánica, obsérvese que es mas general que el principio de conservación de la energía mecánica, la energía mecánica solo se conserva cuando las fuerzas interiores son conservativas.
El principio de conservación de la cantidad de movimiento se cumple cualquiera que sea la naturaleza de las fuerzas interiores.
EJEMPLOS
En la siguiente figura, se muestra un cuerpo A de masa ma, que se mueve hacia la derecha sobre una superficie lisa horizontal, con velocidad Va1 y choca con un segundo cuerpo B de nasa mb, el cual se mueve hacia la izquierda con velocidad Vb1.
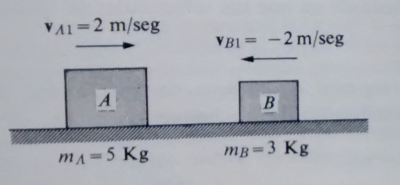
Dado que no hay rozamiento y que la fuerza vertical resultante sobre el sistema es nula, las únicas fuerzas sobre los cuerpos son interiores de acción y reacción que ejercen uno sobre el otro durante el proceso del choque, por lo cual la cantidad de movimiento del sistema permanece constante tanto en magnitud como en dirección y sentido.
Sean VA2 y VB2 las velocidades de A y B después del choque se obtiene.
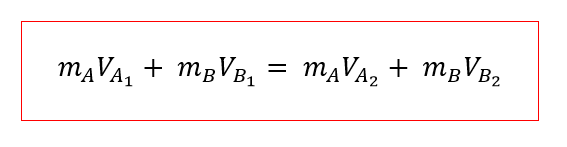
REFERENCIAS
- Libro FISICA FRANCIS W.SEARS y MARK W. ZEMANSKY
- Wikipedia
Si quieres conocer otros artículos parecidos a IMPULSO Y CANTIDAD DE MOVIMIENTO puedes visitar la categoría Fisica.





Deja un comentario